Дробь — это математическая операция, которая позволяет представить число в виде отношения двух целых чисел. В общем случае, дробь состоит из числителя и знаменателя, где числитель указывает на количество частей, а знаменатель — на количество частей, на которые число разделено. Например, 1/2 означает, что целое число разделено на две равные части, а 2/3 — на три равные части.
Данный материал посвящен просвещению в области обыкновенных дробей. В нем будут приведены примеры использования дробей в различных ситуациях, а также инструкция по использованию клавиатуры для ввода дробей и общий урок по дополнительным математическим операциям с обыкновенными дробями.
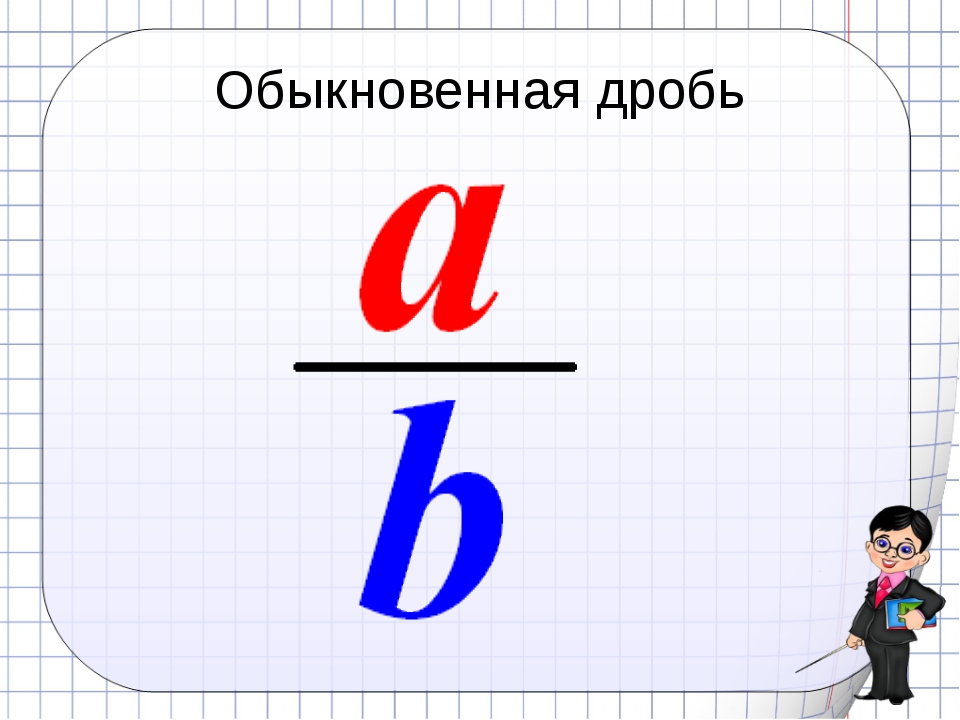
Обыкновенная дробь представляет собой дробное число, в котором числитель и знаменатель являются натуральными числами. В случае, если числитель больше знаменателя, такую дробь называют «смешанной дробью». В качестве примера, можно привести дробь 3 1/2, где число 3 — целая часть, а дробь 1/2 — дробная часть числа.
Обыкновенные дроби
Обыкновенные дроби широко используются в математике и имеют большое значение в решении различных задач. Они позволяют нам работать с числами, которые не являются натуральными или целыми, а также выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление.
Числитель и знаменатель
Числитель — это число, которое находится в верхней части дроби, а знаменатель — число, которое находится в нижней части дроби. Например, в дроби 3/5 числитель равен 3, а знаменатель равен 5.
Ввод и использование
Обыкновенные дроби можно вводить с помощью клавиатуры или калькулятора, а также использовать в различных вычислениях и задачах. Например, если мы хотим узнать, какая часть от целого представляет собой дробь, мы можем использовать обыкновенную дробь для выражения этой доли.
Операции с обыкновенными дробями
С обыкновенными дробями можно выполнять такие арифметические операции, как сложение, вычитание, умножение и деление.
- Сложение: для сложения двух дробей их знаменатели должны быть равными. Если знаменатели различны, то дроби следует привести к общему знаменателю.
- Вычитание: вычитание обыкновенных дробей выполняется аналогично сложению, но с использованием операции вычитания.
- Умножение: для умножения обыкновенных дробей умножаем их числители, а затем знаменатели.
- Деление: для деления одной обыкновенной дроби на другую, умножаем первую дробь на обратную второй дроби.
При выполнении операций с обыкновенными дробями необходимо обращать внимание на правильное использование знаков и представление полученного результата в виде обыкновенной дроби.
Также стоит отметить, что обыкновенные дроби могут быть эквивалентными, то есть иметь одно и то же числовое значение, но разные представления с разными числителями и знаменателями.
В уроке по обыкновенным дробям будут рассмотрены дополнительные возможности использования и вычисления с дробями.
Калькулятор дробей
Перед вводом дроби в калькулятор, сначала нужно представить дробь в числителе и знаменателе. Например, если у нас есть обыкновенная дробь «девять девятых», то мы представляем ее как 9/9. Использование цифровых кнопок на клавиатуре позволяет вводить числитель и знаменатель дроби.
Калькулятор дробей также имеет дополнительные возможности, такие как смешанные числа и использование скобок. В общем случае, для использования калькулятора дробей следует следовать инструкции, которые приведены на экране во время ввода дроби. В случае использования скобок, мы можем применять операции сложения, вычитания, умножения и деления к обыкновенным дробям внутри скобок.
Основные операции, такие как сложение, вычитание, умножение и деление обыкновенных дробей, а также их сокращение, приведены в материалах урока по обыкновенным дробям. Для повторения этих вычислений мы можем использовать функции калькулятора дробей.
Калькулятор дробей предоставляет возможность следующих действий:
- Сложение обыкновенных дробей
- Вычитание обыкновенных дробей
- Умножение обыкновенных дробей
- Деление обыкновенных дробей
- Сокращение обыкновенных дробей
В примере использования калькулятора дробей, мы должны ввести две обыкновенные дроби, а затем выбрать операцию, которую хотим выполнить. Калькулятор дробей автоматически выведет результат на экран.
Использование калькулятора дробей позволяет решать различные задачи, связанные с обыкновенными дробями, такие как вычисление суммы товаров, разделение чего-либо на равные части и т.д. Калькулятор дробей делает вычисления с обыкновенными дробями более простыми и удобными.
Дополнительные возможности калькулятора дробей
При использовании калькулятора дробей по инструкции, вы можете выполнять различные операции с обыкновенными дробями.
- Сложение и вычитание: для сложения двух обыкновенных дробей, сначала введите числитель и знаменатель первой дроби, затем введите числитель и знаменатель второй дроби. Разность будет автоматически вычислена и представлена в виде обыкновенной дроби с общим знаменателем.
- Умножение: для умножения двух обыкновенных дробей, введите числитель и знаменатель первой дроби, затем введите числитель и знаменатель второй дроби. Произведение будет представлено в виде обыкновенной дроби с перемноженными числителями и знаменателями.
- Деление: для деления двух обыкновенных дробей, введите числитель и знаменатель первой дроби, затем введите числитель и знаменатель второй дроби. Частное будет представлено в виде обыкновенной дроби с числителем первой дроби, умноженным на знаменатель второй дроби, и знаменателем первой дроби, умноженным на числитель второй дроби.
Также калькулятор дробей имеет дополнительные возможности:
- Ввод числовых данных: калькулятор позволяет вводить обыкновенные дроби и числа, а также натуральные числа и смешанные числа с помощью цифровой клавиатуры.
- Повторение предыдущих вычислений: калькулятор сохраняет историю выполненных операций, так что вы можете повторить предыдущие вычисления или использовать результаты в новых задачах.
Изучение и использование обыкновенных дробей — важный урок в просвещении о числах. Дополнительные возможности калькулятора дробей позволяют легче изучать тему «обыкновенные дроби», если было трудно представить сложение, вычитание, умножение или деление дробью с общими знаменателями.
Ввод данных в калькулятор дробей
Для работы с обыкновенными дробями необходимо знать, как представить дроби числами. Обыкновенная дробь состоит из числителя и знаменателя, и для использования в калькуляторе дробей необходимо ввести оба этих числа.
При вводе дробей в калькуляторе дробей следует предусмотреть возможность использования цифровой клавиатуры. Если знаменатель дроби является натуральным числом, то в калькуляторе следует нажать на клавишу соответствующей цифры, а затем на клавишу с символом «/», чтобы разделить числитель и знаменатель.
В случае, если числитель и знаменатель обыкновенной дроби являются натуральными числами, можно использовать дополнительные клавиши на клавиатуре калькулятора. Например, для ввода дроби 2/3 можно нажать на клавиши «2», «/», «3».
Для ввода дроби смешанного числа, которое состоит из натуральной части и дробной части, необходимо сначала ввести натуральное число, затем символ «/», а затем ввести числа числителя и знаменателя дроби. Например, для ввода числа 1 3/4 следует нажать на клавиши «1», «/», «3», «/», «4».
При вводе дробей в калькуляторе дробей всегда следует обратить внимание, чтобы знаменатель не был равен нулю. В случае, если знаменатель обыкновенной дроби равен нулю, деление на ноль невозможно и ошибку следует исправить.
Примеры ввода данных:
| Ввод | Дробь |
|---|---|
| 2/5 | Две пятых |
| 1/2 | Одна вторая |
| 3/4 | Три четверти |
| 4/9 | Четыре девятых |
В своих уроках по материалам просвещения и решения задач по обыкновенным дробям следует использовать калькулятор дробей для упрощения вычислений и получения числовых значений дробей.
Онлайн калькулятор дробей
Для выполнения различных вычислений с обыкновенными дробями всегда можно использовать удобные онлайн калькуляторы. Это позволяет значительно упростить работу с разнообразными математическими операциями, связанными с дробями.
При работе с обыкновенными дробями сначала необходимо сделать некоторые преобразования для удобства вычислений. Например, в случае смешанных дробей, где есть целое число и правильная дробь, их можно представить в виде обычной дроби, где числитель — это произведение целого числа на знаменатель плюс числитель, а знаменатель остается тот же.
Для умножения или деления обыкновенных дробей можно использовать следующий общий метод: перемножаем числители и знаменатели дробей, получая числитель и знаменатель произведения. При этом в случае умножения дробей, все дополнительные материалы по преобразованию дробей приводят к общим знаменателям. В случае деления дробей приводят к одной дроби и делят числитель одной дроби на знаменатель другой.
Для сложения и вычитания обыкновенных дробей с одинаковыми знаменателями достаточно складывать (вычитать) числители и оставлять знаменатель неизменным.
При использовании цифровых калькуляторов с функцией работы с обыкновенными дробями следует сначала ввести числитель, затем знаменатель через дробную черту на клавиатуре. Если числитель больше знаменателя, то можно использовать клавишу «>», чтобы ввести знаменатель.
В общем случае при вводе десятичных чисел на калькуляторе онлайн следует помнить, что они являются приближенными значениями для дробных чисел. Поэтому для точных вычислений с обыкновенными дробями лучше использовать натуральные числа в числителе и знаменателе.
Вычисления с дробями. Сложение, вычитание, умножение и деление дробей.

При вычислениях с дробями, также как и при работе с целыми числами, можно выполнять сложение, вычитание, умножение и деление.
1. Сложение и вычитание дробей
Для сложения и вычитания дробей их знаменатели должны быть одинаковыми. Если знаменатели разные, то их надо привести к общему знаменателю. Затем сложение или вычитание числителей дает общий числитель, а знаменатель остается таким же.
2. Умножение дробей
Умножение дробей производится перемножением числителей и знаменателей. Полученный числитель и знаменатель дроби называют общим числителем и общим знаменателем.
3. Деление дробей
Деление дробей выполняется умножением первой дроби на обратную второй дробь. Для получения обратной дроби числитель и знаменатель дроби меняются местами. Затем следует выполнить умножение дробей по правилу, указанному в пункте 2.
Примеры вычислений с дробями:
Пример сложения дробей:3/4 + 2/5 = (3 * 5) / (4 * 5) + (2 * 4) / (5 * 4) = 15/20 + 8/20 = (15 + 8) / 20 = 23/20
Пример вычитания дробей:2/3 - 1/4 = (2 * 4) / (3 * 4) - (1 * 3) / (4 * 3) = 8/12 - 3/12 = (8 - 3) / 12 = 5/12
Пример умножения дробей:2/5 * 3/4 = (2 * 3) / (5 * 4) = 6/20
Пример деления дробей:2/3 / 1/4 = (2/3) * (4/1) = (2 * 4) / (3 * 1) = 8/3
При работе с дробями можно использовать как обыкновенные дроби, так и смешанные дроби. Смешанные дроби состоят из натуральной части и дробной части (дробей с числителем меньшим знаменателя). Для работы с смешанными дробями сначала надо привести их к общему знаменателю.
Существуют различные способы выполнения вычислений с дробями. Одним из них является использование калькулятора. Для операций сложения, вычитания, умножения и деления дробей можно воспользоваться онлайн калькулятором, вводя числа и знаки операций с помощью клавиатуры.
Инструкция по использованию онлайн калькулятора для работы с дробями:
- На калькуляторе выбираем режим работы с дробями.
- Вводим числитель первой дроби.
- Вводим знаменатель первой дроби.
- Вводим знак операции (+, -, *, /).
- Вводим числитель второй дроби.
- Вводим знаменатель второй дроби.
- Нажимаем на кнопку «Вычислить».
- Результат вычисления будет выведен на экран.
Повторение по вычислениям с дробями и использованию калькулятора поможет лучше разобраться в данном материале и успешно решать задачи, связанные с обыкновенными дробями.
Дополнительные возможности калькулятора для работы с дробями:
В калькуляторе можно вводить дроби с цифровой клавиатуры, а также использовать пунктуационные клавиши (точка и запятая) для разделения чисел с плавающей точкой.
При вводе дроби необходимо сначала ввести числитель, затем знаменатель, разделяя их символом «/». Если числитель равен нулю, то дробь будет равна нулю.
Таким образом, вычисления с обыкновенными дробями – это одна из важных тем, которую следует изучать в школе. С помощью материала, представленного выше, урок по обыкновенным дробям станет более понятным и интересным.
Источник: учебник «Математика для 5 класса» Чулков А. В., Издательство «Просвещение».
Инструкция использования калькулятора дробей
При использовании калькулятора дробей важно правильно вводить данные. При вводе дроби следует разделять числитель и знаменатель знаком «/». Например, для представления числа девять в виде дроби, необходимо ввести «9/1».
Калькулятор дробей обеспечивает возможность выполнения различных операций над обыкновенными дробями. В том числе, вы можете выполнять следующие действия: сложение, вычитание, умножение и деление.
Для сложения или вычитания двух обыкновенных дробей с одинаковыми знаменателями, достаточно просто добавить или вычесть числители. Знаменатель остается неизменным.
В случае, если знаменатели дробей различны, перед сложением или вычитанием необходимо привести дроби к общему знаменателю. Для этого необходимо умножить числитель и знаменатель каждой дроби на знаменатель другой дроби.
Операции умножения и деления обыкновенных дробей производятся путем перемножения или деления числителей, а затем знаменателей. Результат умножения или деления всегда будет обыкновенной дробью.
Дополнительные задачи, такие как упрощение обыкновенных дробей, нахождение разности или приведение к общему знаменателю, могут быть выполнены с использованием калькулятора дробей.
Всегда помните, что калькулятор дробей предоставляет возможности для вычислений с обыкновенными дробями. Он упрощает процесс математического расчета и обеспечивает дополнительное просвещение по темам дробей и их использования в натуральных числах.
Числитель и знаменатель дроби
Обыкновенные дроби представляют собой числитель и знаменатель. Числитель обозначает количество частей, на которые разделено целое число или представленная фигура, а знаменатель указывает на количество этих частей.
Числитель и знаменатель дроби должны быть целыми числами и не иметь общих делителей, кроме единицы.
Числитель
Числитель обыкновенной дроби обычно приведен в виде числа, которое указывает, сколько частей из общего количества частей изображается или представляется этой дробью.
Знаменатель
Знаменатель обыкновенной дроби представляет собой число, которое указывает, на сколько частей общего количества разделена единица или представленная фигура при использовании этой дроби.
При выполнении операций с дробями, такими как сложение, вычитание, умножение, деление или сравнение, необходимо общий знаменатель. Если знаменатели обыкновенных дробей разные, их нужно привести к общему знаменателю, чтобы произвести операции.
Существуют онлайн калькуляторы, которые могут помочь в вычислениях с обыкновенными дробями. Их использование упрощает работу с числами и позволяет быстро получить результат.
